Impedancja (Z = R + XC + XL) [Ohm] – wartość zespolona na którą składa się rezystancja oraz reaktancja pojemności (kondensatora) i indukcyjności (cewki).
Admitancja (Y = G + jB) [Simens] – odwrotność impedancji. Jej składowe to rzeczywista konduktancja i urojona susceptancja.
Rezystancja (R) [Ohm] – część rzeczywista impedancji, opór czynny, prąd płynący w fazie z napięciem.
Reaktancja (X = XC + XL) [Ohm] – część urojona impedancji, opór bierny, prąd płynący z przesunięciem w fazie o 90 stopni względem napięcia. Ujemna reaktancja, nazywana jest też kapatancją. Dodatnia reaktancja to z kolei induktancja.
Zawada (|Z|) [Ohm] – moduł/długość impedancji w formie liczby rzeczywistej.
Kondensator – element obwodu elektronicznego stanowiący rozwarcie dla prądu stałego. Przewodzi prąd przemienny tym lepiej im większa jest jego częstotliwość. Reaktancja kondensatora jest zawsze ujemna i oblicza się ją ze wzoru:
XC = -j * (1/ωC) = -j * (1/2πfC),
gdzie j to jednostka urojona, ω to pulsacja, C to pojemność kondensatora, a f to częstotliwość.
Pojemność kondensatora: C (pojemność) = Q (ładunek) / U (napięcie) [Farad = Kulomb/Volt]
Kondensatory można łączyć szeregowo i równolegle, a ich zastępczą pojemność oblicza się odwrotnie niż zastępczą rezystancję połączonych szeregowo/równolegle rezystorów.
Cewka – element obwodu elektronicznego stanowiący zwarcie dla prądu zmiennego. Stawia “opór” dla prądu przemiennego tym większy im wyższa jest jego częstotliwości. Reaktancja cewki jest zawsze dodatnia i oblicza się ją ze wzoru:
XL = jωL = j2πfL,
gdzie j to jednostka urojona, ω to pulsacja, L to indukcyjność cewki, a f to częstotliwość.
Indukcyjność cewki wyrażamy w Henrach. Cewki można łączyć szeregowo i równolegle, a ich indukcyjność wylicza się wtedy podobnie jak rezystancję połączonych szeregowo/równolegle rezystorów.
Liczby zespolone
z = A+jB = zejφ
z = |z| = sqrt( A2+B2 )
φ = arg z
j2 = -1 // jednostka urojona
tg(φ) = B/A
cos(φ) = A/Z
sin(φ) = B/Z
z* = A-jB // liczba przeciwna
z*(z*) = A2+B2 = z2
zn = zejnφZamiana na postać symboliczną
v(t) = Vm * sin( ωt + φ )
v(t) - wartość chwilowa w chwili t
Vm - amplituda - wartość maksymalna
ω - pulsacja (do obliczeń metodą symboliczną t=0)
φ - faza początkowa
V = Vm/sqrt(2) * ejφ
Vm/sqrt(2) - wartość skuteczna napięcia
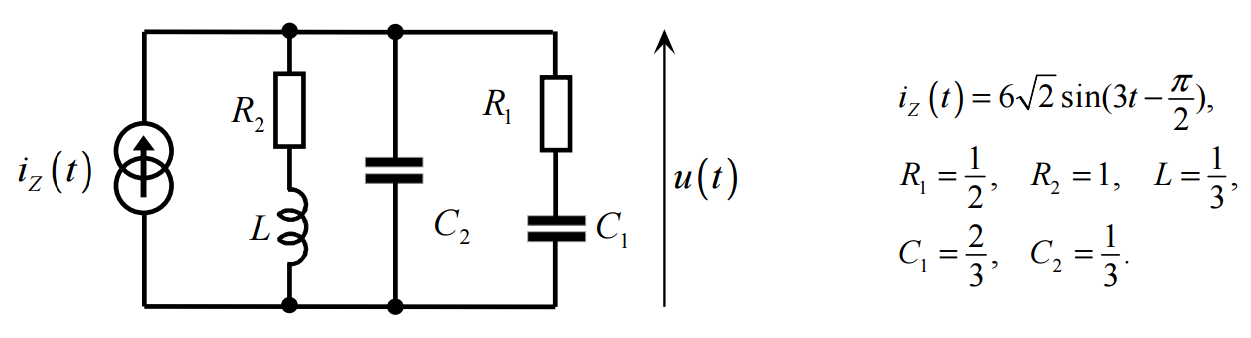
Przykład
iZ(t) = 6*sqrt(2) * sin( 3t - π/2 )
I = 6e-j(π/2)
I = -6j
ω = 3
U = Z*I
Z1 = R1 - j/(ωC1) = 0.5 - j/(3*[2/3]) = 0.5 - 0.5*j
Z2 = -j/(ωC2) = -j/(3*[1/3]) = -j
Z3 = R2 + jωL = 1 + j*3*(1/3) = 1 + j
Y1 = 1/(0.5 - 0.5*j)
Y1 = (0.5 + 0.5*j) / [(0.5 - 0.5*j)*(0.5 + 0.5*j)]
Y1 = (0.5 + 0.5*j) / [0.25 + 0.25*j - 0.25*j + 0.25]
Y1 = (0.5 + 0.5*j) / 0.5
Y1 = 1 + j
Y2 = -1 / j = (-1)*(-j) / j*(-j) = j/(-j2) = j
Y3 = 1/(1 + j)
Y3 = (1 - j)/[(1 + j)*(1 - j)]
Y3 = (1 - j)/[1 - j + j + 1]
Y3 = (1 - j)/2
Y3 = 0.5 - 0.5*j
ZC = 1/[ 1 + j + j + 0.5 - 0.5*j ]
ZC = 1/(1.5 + 1.5j)
ZC = (1.5 - 1.5j)/[(1.5 + 1.5j)*(1.5 - 1.5j)]
ZC = (1.5 - 1.5j)/[2.25 - 2.25j + 2.25j + 2.25]
ZC = (1.5 - 1.5j)/4.5
ZC = (1/3) - (1/3)*j
U = Z*I
U = [(1/3)-(1/3)*j] * (-6j)
U = -2 -2j
U = 2*sqrt(2) * e-j(3/4)π
u(t) = 4 * sin(3t - (3/4)π)